Wet-sieving Model

Modelling the breakdown and distribution of aggregates in the wet-sieving method (using nested sieves)

Theory

Fig. 1 illustrates the breakdown and movement of aggregates in a nest of three sieves during wet-sieving (Yoder, 1936; Kempil and Chepil, 1965), where i denotes the sieve number (i = 1 to n) where sieve 1 is the sieve with the largest aperture size, followed by sieve 2, and so on. Note that the sieve n (last sieve) refers to the container that holds the water and the nest of sieves.

Fig. 1. Simultaneous breakdown and movement of aggregates in the various sieves

Original aggregates are aggregates that were placed in each sieve before wet-sieving, and ruptured aggregates are those that had ruptured during wet-sieving (Fig. 1). The weight of the original aggregates in sieve i is Wai, and the weight of all retained aggregates in sieve i after wet-sieving is Wbi. The weight of ruptured aggregates from aggregate size fraction i is bi,i+1,i+2,…,n, where the subscripts denote the path of ruptured aggregates in the nested sieves. b1,2, for example, is the weight of ruptured aggregates from sieve 1 in sieve 2; and b1,2,3 is the weight of ruptured aggregates from sieve 1, settling in sieve 2 before further breaking down and settling in sieve 3. Note that bi,i (equal subscripts) denotes the weight of original aggregates in sieve i; for example, b1,1 is Wa1, b2,2 is Wa2, and b3,3 is Wa3.

Aggregates retained in a given sieve after wet-sieving are referred as retained aggregates, and its weight wi,…,j in sieve j can be calculated by

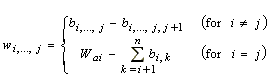(1)

where wi,…,j is the portion of bi,…,j or Wai remaining in sieve j (i >= j). For example, w1,2,3 or (b1,2,3 - b1,2,3,4) is the portion of b1,2,3 that remained in sieve 3, and w2,2 or (Wa2 - b2,3 - b2,4) is the portion of Wa2 that remained in sieve 2. Note that wi,i (equal subscripts) is the weight of the intact aggregates (Fig. 1) and the weight of these aggregates must be known to determinate the stability of an aggregate size fraction. This is because the stability of aggregate size fraction i (ASi) in percent is calculated by

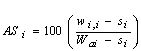(2)

where si is the weight of sand particles larger than the aperture size of sieve i.

The total weight of aggregates that have passed through sieve i is Di (Fig. 1), where Di is calculated by

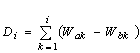(3)

The weight of ruptured aggregates are related to Di by

		(4)
		(5)
		(6)

In the three independent equations Eq. (4) to (6), there are 11 unknowns: b1,2, b1,3, b1,4, b1,2,3, b1,2,4, b1,3,4, b1,2,3,4, b2,3, b2,4, b2,3,4 and b3,4. To reduce the number of unknowns, it is assumed that ruptured aggregates of the same size fraction (same sieve) have equal weights, provided they are from the same origin (i.e., they are pieces from the same original aggregates). This assumption means

(7)

Thus,

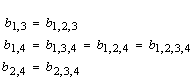The validity of Eq. (7) is uncertain; however, model testing done later in this study would determine if the use of Eq. (7) is at least reasonable.

Using Eq. (7), the weight of ruptured aggregates are now related to Di by

		(8)
		(9)
		(10)

which can be summarised to 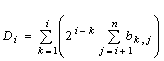. The number of unknowns in the three equations have now been reduced to six: b1,2, b1,3, b1,4, b2,3, b2,4 and b3,4. To further reduce the number of unknowns, it is assumed that aggregates of the same size fraction would break down equally in percentage. This assumption is reasonable because aggregates of the same size fraction belonging to the same soil sample can be regarded to breakdown equally in percentage. Using this assumption means that

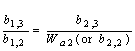		(11)
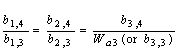		(12)
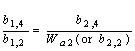		(13)

which can be summarised to 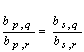. By substituting Eq. (11) to (13) into Eq. (9) and (10), it can be shown that Eq. (9) and (10) are re-expressed to

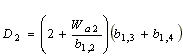		(14)
		(15)

The number of unknowns in the three equations have now be reduced to three: b1,2, b1,3 and b1,4; thus, Eq. (8),(14) and (15) are solvable. The calculated b1,2, b1,3 and b1,4 are substituted back into Eq. (7), and Eq. (11) to (13) to determine b1,2,3, b1,2,4, b1,3,4, b1,2,3,4, b2,3, b2,4, b2,3,4 and b3,4.

Finally, it can be shown that the general equation to determine the weight of the ruptured aggregates (b1,i >= 0) for any number of sieves is calculated by

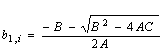(16)

where

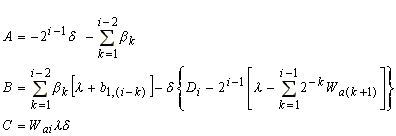with

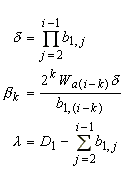As an example: the parameters A, B and C for b1,3 would be (-2Wa2 - 4b1,2), (2D1Wa2 + 4D1b1,2 - D3b1,2 - 2Wa2b1,2 - Wa3b1,2 - 4b1,2b1,2), and (D1Wa3b1,2 - Wa3b1,2b1,2), respectively.

References

Kemper, W.D. and W.S. Chepil, 1965. Size distribution of aggregates. In: Black, C.A. (ed.), Methods of soil analysis. part 1, Agronomy. No. 9, ASA, Madison, WI, pp. 499-510.

Yoder, R.E. 1936. A direct method of aggregate analysis of soils and a study of the physical nature of erosion losses. J. Amer. Soc. Agron. 28: 337-351.

Excel Spreadsheet

You can download the following Excel 97 spreadsheet that demonstrates the above calculations for a nest of seven sieves (the last "sieve" is the container).

Wet-sieving model: demonstration file

demo.xls (271 kb)